Memorizing Multiplication Tables and Math Facts

Thoughts from a history teacher

Welcome! I'm Lauren Brown and this is my newsletter on education issues that impact all of us— students, parents, educators & concerned citizens.

I recently wrote a piece for MiddleWeb about memorizing the 50 states explaining why I decided to have my 7th graders memorize the 50 states last year, and what I learned from that experience.

An opinion piece by Chad Aldeman in The74, “No Textbooks, Times Tables or Spelling Tests: Things My 6th Grader Didn’t Learn,” was the inspiration for my article and got me thinking about the connection between knowing the 50 states and memorizing the multiplication times tables. Productive discussions between math and social studies educators could lead to significant positive outcomes. This post is an initial effort to do that.

One starting point might be to consider the research on cognitive load theory and other cognitive processes that I was first introduced to through the work of cognitive psychologist Daniel Willingham. Getting information into your long-term memory, even if you have to memorize it to make it happen, frees up the brain to learn new information. Teachers are routinely bombarded with the message that we should avoid requiring “rote knowledge”¹ and that teaching facts is a waste of time when kids can just Google the answers. While memorizing facts shouldn't be the sole focus of education, a strong foundation of knowledge is essential for deeper learning.

What follows are a few observations of student struggles with math in history class.

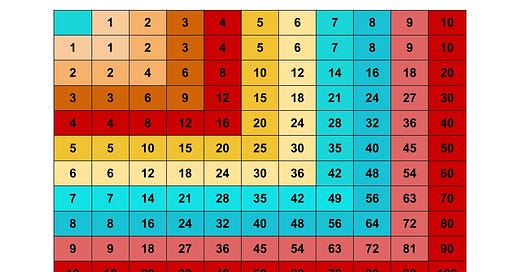
In a lesson with 8th graders on westward expansion and conflict with Native Americans on the Plains, I show students the chart below with the question on the left.

Many students quickly jump to say that 1800 to 1850 was the largest decline, confusing percentage with raw numbers, not to mention skimming past the fact that this happened over the course of 50 years. While in fact, the greatest percentage decline is from 1885-1889, a period of only 4 years, with the period of 1870-1875 following close behind. This coincides with the height of the Indian Wars in the Plains and is a data point that underscores deliberate efforts to decimate the bison population in order to weaken the strength of Native Americans in this region.

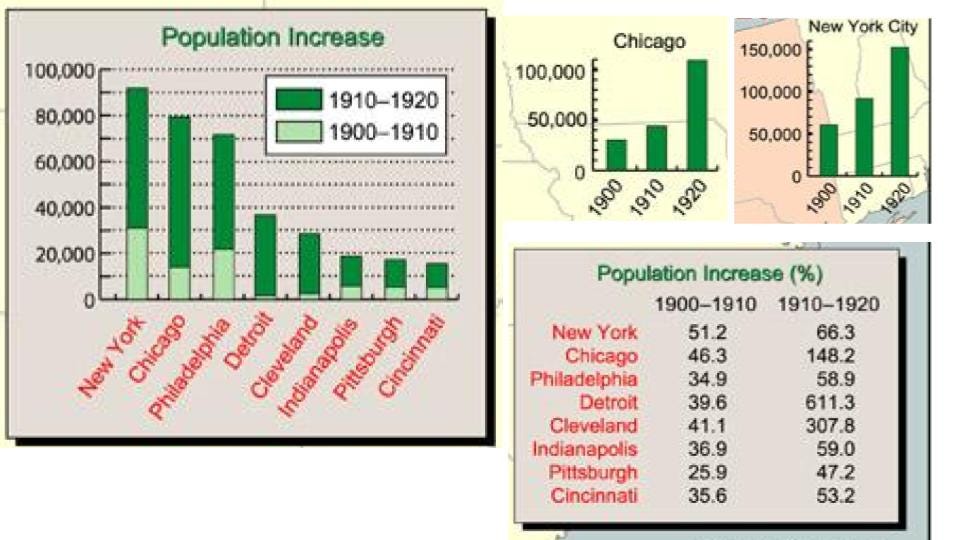
In this next example, my 8th graders are often confused about this question: in which cities did the population of African Americans grow the fastest at the beginning of the 20th century? Many answer with New York as #1, confusing the fact that New York had the largest population of African Americans with the fact that Detroit’s population of African American grew the fastest.

Over the years, I have observed even more concerning examples of math struggles. Confusion involving simple subtraction when discussing how long ago something happened in history, like the onset of the Depression to the start of World War II. Students getting out their calculators to add the number of representatives in the House (435) to the number of Senators (100) plus 3 for Washington, D.C. to get to the total of 538 in the Electoral College. Watching kids get out their calculator while doing their math homework in advisory in order to figure out 5 x 100.

I am not a math teacher, nor am I particularly good at math, though I hate to say that, cognizant of all the social and cultural baggage surrounding such a statement.² But I can do every one of the examples above easily, in my head, and our students ought to be able to do this as well. I also want to be clear that I am not blaming the math teachers. When I have pointed out these examples to math teachers I have worked with, they sigh and agree with me.

So I am left wondering if the same issues I have as a history teacher— that kids just aren’t being taught enough basic stuff— are also a problem for math teachers? If so, we need to think more carefully about how we teach math and number sense from the beginning. Not just K-5, but even in preschool. Facts are helpful.

The names of the 50 states and at least some of the multiplication tables are just two examples. It should go without saying that eventually students should move on from memorization and basic math facts to more advanced work that includes problem-solving and creativity.³

So should we ask kids to memorize the 50 states?

Sure. Memorizing that is not a big deal; my students were able to do it, and others can too. While memorizing is not a big deal, knowing the basic geography of the country is—this knowledge provides background, context and a starting point for learning more.

And do they need to memorize their times tables?

Math teacher, Michael Pershan addresses this question thoughtfully in a post on his Substack, “Just How Helpful is Knowing Your Multiplication Facts?” Dylan Kane commented on the post, pointing out that he can effectively teach “if students just know 2s, 3s, 4s, 5s, and 10s really well.”⁴

I will leave the specifics to the math teachers to debate. It is a debate worth having in every subject area. Content matters. Taking out calculators for basic arithmetic is a time waster. When there is so much to learn—so many beautiful, interesting things to learn—it feels like an avoidable distraction.

1. Check out Daniel Willingham, “Ask the Cognitive Scientist: Inflexible Knowledge: The First Step to Expertise,” for a careful look at the difference between rote and inflexible knowledge.

2. This is more likely to be an issue in Western societies. Interestingly, it is culturally acceptable to be “bad at math,” while being a poor reader is more stigmatized. When we casually say, “oh, I’m just not good at math” it reinforces the false idea that math ability is innate and can’t be developed. In other words, it’s a cop-out.

3. Jerry Burkhart, who I discovered from his insightful article at MiddleWeb, is an educator whose work seems worth exploring. You can find a few more articles from Jerry here and here.

4. I was inspired to read a bit more about math education. Here are a few articles representing just the tip of the iceberg. From Edweek: Kids Need to Know Their Math Facts. From Substack: Just How Helpful is Knowing Your Multiplication Facts? (referenced above) and Mathematics teachers who don’t like mathematics. Hidden Skills is a wonderful piece by Dylan Kane that explains how not knowing about inverse operations holds students back later on in math class. He writes about that in a more general sense at the end of his piece, “Math is Awesome.” From cognitive psychologist Daniel Willingham: Is It True That Some People Just Can’t Do Math? And this blogpost from math teacher Barry Garelick. I’d also suggest work from Sunil Singh on Medium. And an update 3/17/25: wish I read this article before I wrote this post!

Should we teach children to memorize the multiplication tables?